# CS 5220: Applications of Parallel Computers
## Matmul and tiling
## 08 Sep 2015
## A memory benchmark (membench)
for array A of length L from 4KB to 8MB by 2x
for stride s from 4 bytes to L/2 by 2x
time the following loop
for i = 0 to L by s
load A[i]
Membench in pictures
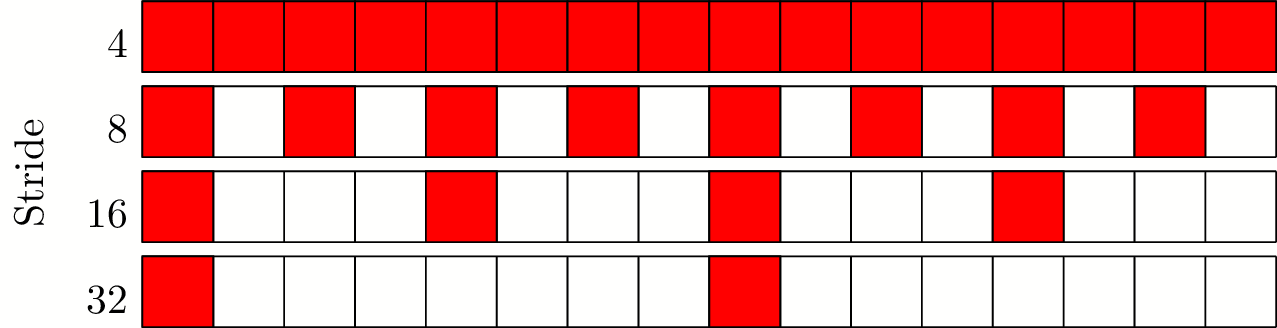
- Size = 64 bytes (16 ints)
- Strides of 4, 8, 16, 32 bytes
Membench on totient CPU

- Vertical: 64B line size, 4K page size
- Horizontal: 64KB L1, 256KB L2, 15MB L3
- Diagonal: 8-way cache associativity, 512 entry L2 TLB
Note on storage
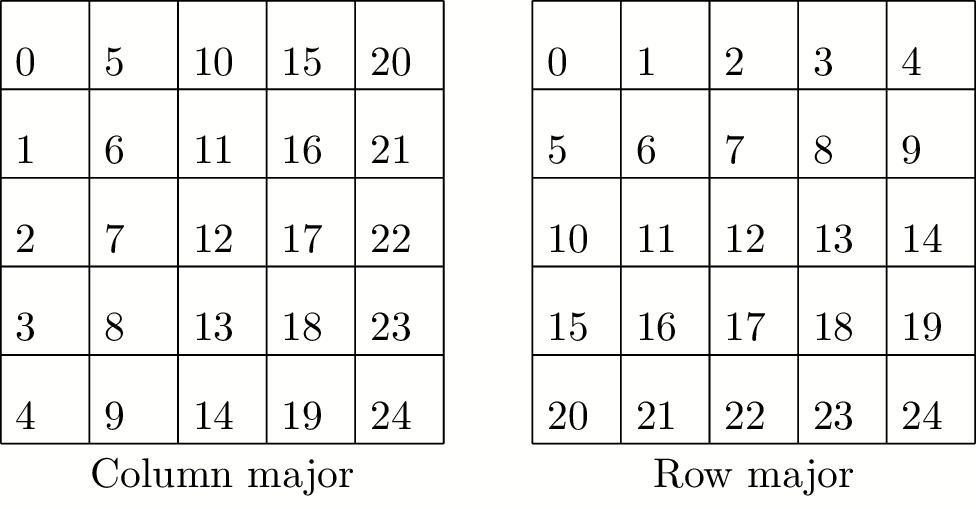
- Two standard layouts:
- Column major (Fortran): A(i,j) at A+i+j*n
- Row-major (C): A(ij) at A+i*n+j
- I default to column major
- Also note: C has poor language matrix support
## Matrix multiply
How fast can naive matrix multiply run?
#define A(i,j) AA[i+j*n]
#define B(i,j) BB[i+j*n]
#define C(i,j) CC[i+j*n]
memset(C, 0, n*n*sizeof(double));
for (int i = 0; i < n; ++i)
for (int j = 0; j < n; ++j)
for (int k = 0; k < n; ++k)
C(i,j) += A(i,k) * B(k,j);
One row in naive

- Access $A$ and $C$ with stride $8n$ bytes
- Access all $8n^2$ bytes of $B$ before first re-use
- Poor arithmetic intensity
Matrix multiply compared (Totient + ICC)

Hmm...

- Compiler makes some difference
- Naive Fortran is faster than naive C
- Local instruction mix sets
speed of light
- Access pattern determines how close we get to limit
Engineering strategy

- Start with small
kernel
multiply
- Maybe odd sizes, strange layouts -- just go fast!
- May play with AVX intrinsics, compiler flags, etc
- Deserves its own timing rig
- Use blocking based on kernel to improve access pattern
## Simple model
- Two types of memory (fast+slow)
- $m$ = words read from slow memory
- $t_m$ = slow memory op time
- $f$ = number of flops
- $t_f$ = time per flop
- $q = f/m$ = average flops/slow access
- Time:
$$ft_f + mt_m = ft_f \left( 1 + \frac{t_m/t_f}{q} \right)$$
- Larger $q$ means better time
## How big can $q$ be?
Level 1/2/3 Basic Linear Algebra Subroutines (BLAS)
1. Dot product: $n$ data, $2n$ flops
2. Matrix-vector multiply: $n^2$ data, $2n^2$ flops
3. Matrix-matrix multiply: $2n^2$ data, $2n^3$ flops
We like to build on level 3 BLAS (like matrix multiplication)!
## Tuning matrix multiply
- [Matmul assignment is up](https://github.com/cornell-cs5220-f15/matmul)
- You will get email with group assignments
- Goal is single core performance *analysis* and *tuning*
- Deliverables
- Report describing strategy and performance results
- Pointer to a repository so we can run a competition
## Possible tactics
- Manually tune some small kernels
- Write an auto-tuner to sweep parameters
- Try different compilers (and flags)
- Try different layouts
- Copy optimization
- Study strategies from past/present classes!
## Warning
- Tuning can be like video games!
- Do spend the time to do a good job
- Don't get so sucked in you neglect more important things






